Pourquoi s’appelle-t-il « régression logistique » et non « classification logistique » ?

Un étudiant en génie informatique trouve des réponses à la science derrière la technologie !

Pourquoi s’appelle-t-il « régression logistique » ?

Algorithmes d’apprentissage automatique

La régression logistique est l’un des algorithmes d’apprentissage automatique les plus populaires utilisés pour la classification binaire, bien que des versions beaucoup plus complexes soient disponibles.

Une question qui touche presque tout le monde est : « Pourquoi s’appelle-t-il ‘Régression logistique’ s’il s’agit d’un algorithme de classification ? Pourquoi n’est-ce pas ‘Classification logistique’ ? »

Dans cet article, nous allons essayer de répondre à cette question à travers un exemple pratique.

Régression vs. Classification

Comprenons d’abord la différence entre la classification et la régression.

Les algorithmes de régression et de classification appartiennent à la catégorie des algorithmes d’apprentissage supervisé, c’est-à-dire que les deux algorithmes utilisent des ensembles de données étiquetés. Cependant, il existe une différence fondamentale entre les deux.

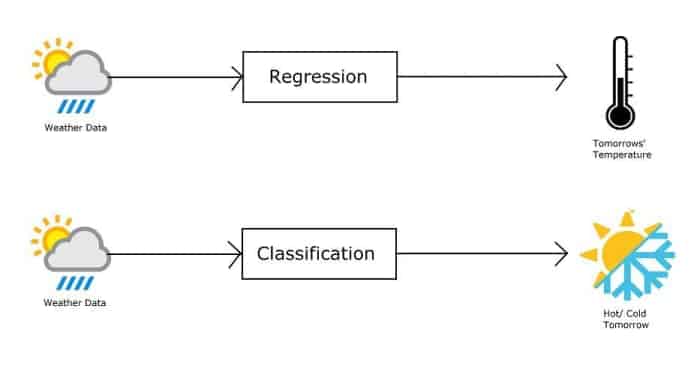
Régression vs. Classification

• Algorithmes de régression sont utilisés pour prédire des valeurs continues telles que la taille, le poids, la vitesse, la température, etc.
• Algorithmes de classification sont utilisés pour prédire/classer des valeurs discrètes telles que fille ou garçon, frauduleux ou juste, spam ou non spam, froid ou chaud, etc.

Par exemple, si nous voulons prédire la température de demain à l’aide d’un ensemble de données météorologiques, nous utilisons un algorithme de régression. Cependant, si nous voulons prédire s’il fera chaud ou froid demain, nous utilisons un algorithme de classification.

Pourquoi la régression linéaire n’est-elle pas adaptée à la classification ?

Essayons de répondre à la question ci-dessus à l’aide d’un exemple. Dans cette section, nous essaierons de classer les tumeurs bénignes/malignes à l’aide d’un algorithme de régression linéaire.

La tâche consiste à classer les tumeurs en catégories bénignes (0) et malignes (1) respectivement. Dès lors, il s’agit d’un classification binaire problème. Pour simplifier, nous avons une variable dépendante—taille de la tumeur—et seulement quelques enregistrements de l’ensemble de données.

La régression linéaire se heurte à deux problèmes majeurs :

1. La régression produit des valeurs continues qui ne peuvent pas être traitées comme purement probabilistes.
2. Il y a un décalage indésirable dans la valeur de seuil lorsque de nouveaux points de données sont ajoutés.

Examinons ces problèmes en détail.

Problème 1 : la sortie n’est pas probabiliste mais continue

Régression linéaire pour la classification – 1

Faites défiler pour continuer

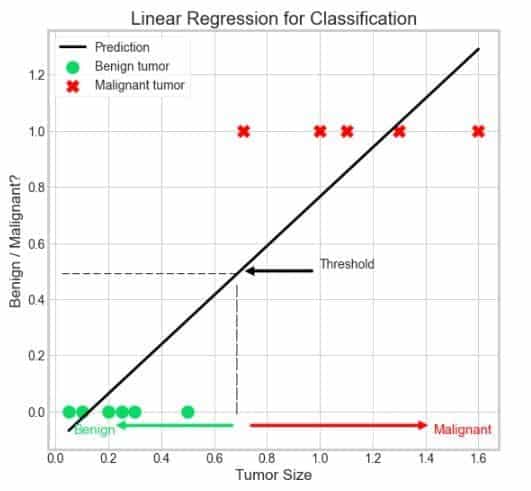
Ci-dessus se trouve notre modèle de régression linéaire formé sur notre ensemble de données. Comme nous l’avons déjà discuté, les algorithmes de régression sont utilisés pour prédire des valeurs continues, c’est-à-dire que la sortie de la régression linéaire est une valeur continue correspondant à chaque valeur d’entrée.

Mais nous voulons que la sortie soit sous la forme de 1 et de 0, c’est-à-dire des tumeurs bénignes et des tumeurs malignes. Ainsi, nous définissons un valeur de seuil0,5 dans ce cas.

Nous pouvons prédire notre sortie comme 1 (maligne) si la sortie de la régression linéaire est supérieure ou égale à la valeur seuil (0,5). De même, si la sortie de la régression linéaire est inférieure à notre valeur seuil, nous pouvons prédire notre sortie comme 0 (bénigne). De cette manière, cette sortie peut être considérée comme la probabilité que la tumeur soit maligne.

Attendez! Nous avons juste raté quelque chose. La probabilité peut-elle être inférieure à 0 ou supérieure à 1 ?

Reportez-vous au tableau ci-dessus, notez que la sortie de la régression linéaire peut être à la fois inférieure à 0 et supérieure à 1. Par conséquent, nous ne pouvons pas traiter cette sortie comme purement probabiliste.

Problème 2 : Décalage indésirable de la valeur de seuil lors de l’ajout de nouveaux points de données

Régression linéaire pour la classification – 2

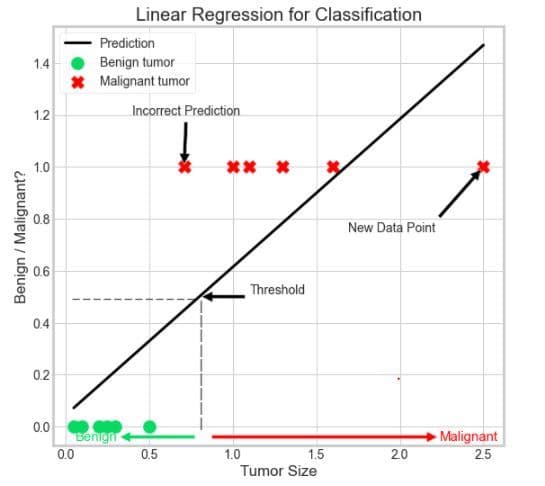
Ici, nous avons introduit un nouveau point de données dans notre jeu de données. Étant donné que la régression linéaire tente de minimiser la différence entre les valeurs prédites et les valeurs réelles, lorsque l’algorithme est formé sur l’ensemble de données ci-dessus, il s’ajuste tout en tenant compte du nouveau point de données ainsi que d’autres points de données.

Cela provoque un décalage de la valeur qui correspond à la sortie de valeur de seuil. Notez que quelques valeurs sont mal prédites maintenant.

Afin de résoudre ces problèmes, nous utilisons la régression logistique.

Fonction logistique

Fonction logistique

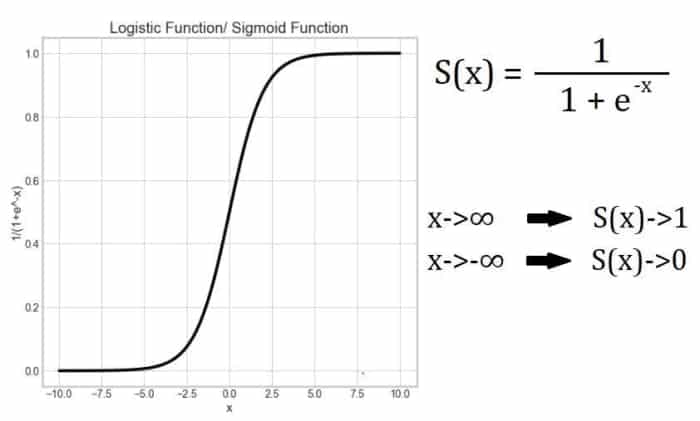
La régression logistique emprunte « logistique » à la fonction logistique. La fonction logistique est également appelée fonction sigmoïde dans le domaine de l’apprentissage automatique. (Il existe un certain nombre de fonctions sigmoïdes telles que la tangente hyperbolique, l’arctangente, etc.)

Cette fonction est une fonction bornée car elle limite/écrase la sortie dans une plage comprise entre 0 et 1. Par conséquent, elle est également connue sous le nom de fonction d’écrasement. Cette propriété le rend utile pour être appliqué dans les algorithmes de classification.

La sortie de la courbe en forme de S est la probabilité que l’entrée appartienne à une certaine classe. Considérons par exemple le problème de la classification d’une tumeur comme bénigne ou maligne. Si la sortie de cette fonction est de 0,85, il y a 85 % de chances que la tumeur soit maligne.

Notez que la fonction asymptote en 0 et 1.

Pourquoi la régression logistique est-elle appelée « régression logistique » et non « classification logistique » ?

Régression linéaire

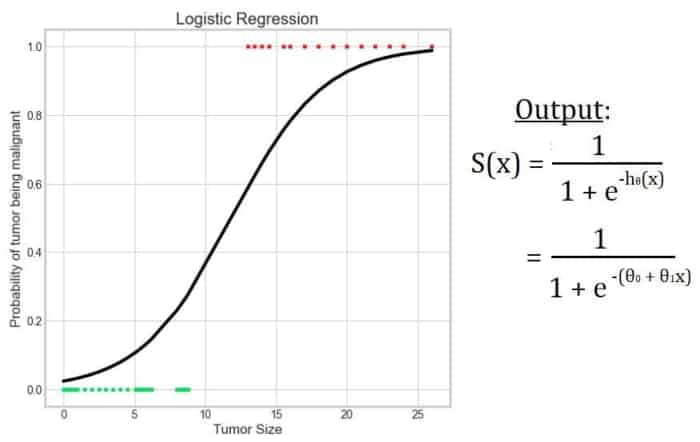
Régression logistique

Après avoir compris les concepts de base, nous sommes tous prêts à surmonter la confusion.

La régression logistique emprunte la « régression » à l’algorithme de régression linéaire car elle utilise sa fonction d’hypothèse.

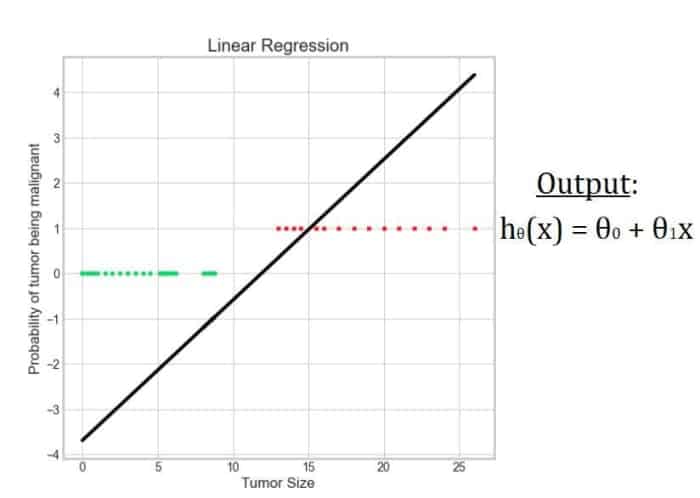
Dans le cas de la régression linéaire, la sortie est la somme pondérée des variables d’entrée.

hθ(x) = θ0 + θ1×1 + θ2×2 + ___ + θnxn

Dans la régression logistique, nous fournissons cette fonction d’hypothèse comme entrée de la fonction logistique.

S(x) = 1 / (1 + e-hθ(x)) = 1 / (1 + e-(θ0 + θ1×1 + θ2×2 + ___ + θnxn))

Par conséquent, il est nommé régression logistique.

Résumé de la régression logistique

• La régression logistique emprunte son nom à la fonction logistique et à l’algorithme de régression linéaire.
• La régression linéaire ne fonctionne pas bien avec les problèmes de classification.
• La régression logistique utilise la fonction logistique qui écrase la plage de sortie entre 0 et 1.
• La régression logistique utilise la fonction d’hypothèse de l’algorithme de régression linéaire.

Vérifiez vos connaissances

Pour chaque question, choisissez la meilleure réponse. La clé de réponse est ci-dessous.

1. La régression logistique est un algorithme ______.
2. La plage de sortie de la fonction logistique est ______.
   • (-ꝏ, )
   • [-1, 1]
   • [0, 1]
   • [-1, 0]
3. La régression linéaire fonctionne très bien pour les problèmes de classification.

Corrigé

1. Classification
2. [0, 1]
3. Faux

Ce contenu est exact et fidèle au meilleur de la connaissance de l’auteur et ne vise pas à remplacer les conseils formels et individualisés d’un professionnel qualifié.

© 2021 Riya Bindra

Umesh Chandra Bhatti de Kharghar, Navi Mumbai, Inde le 02 juin 2021 :

Détail intéressant. Des nouveautés pour moi. Merci.