Un étudiant en génie informatique trouve des réponses à la science derrière la technologie !
Optimisation de la descente de gradient
Passionné de science des données
Qu’est-ce que la descente de gradient ?
Dans cet article, nous allons explorer le fonctionnement de la descente de gradient à travers un exemple pratique de régression linéaire simple.
Pente est la mesure de l’augmentation ou de la diminution de l’ampleur d’une propriété.
Descente indique une baisse de la propriété. L’algorithme Gradient Descent, en termes simples, peut être défini comme un algorithme qui minimise une fonction de coût de manière itérative en modifiant ses paramètres jusqu’à ce qu’il trouve le minimum local.
Avant de nous plonger dans la descente de gradient et son fonctionnement, parlons brièvement de la fonction de coût.
Fonction de coût
La fonction de coût est un moyen de déterminer la précision d’un modèle. Il mesure la séparation entre les valeurs réelles et prédites et l’affiche sous la forme d’un nombre.
En cas de régression, l’écart entre ces valeurs doit être le minimum ce qui implique que la fonction de coût doit être la plus petite possible.
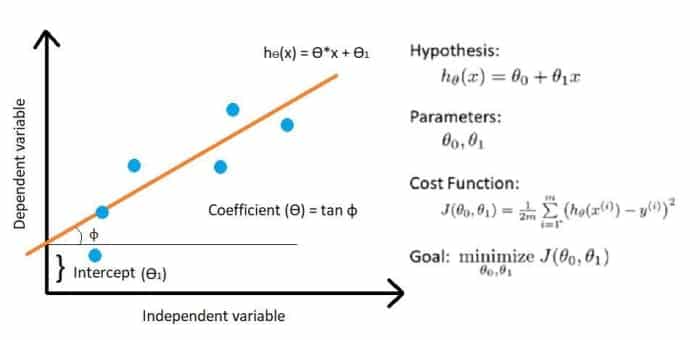
Fonction de coût pour une régression linéaire simple
Fonctionnement de la descente de gradient
La descente de gradient minimise la fonction de coût en mettant à jour simultanément les deux paramètres, coefficient et interception, jusqu’à ce qu’elle trouve le minimum local.
1. Modélisation sans interception
Dans cette section, nous implémenterons la descente de gradient en considérant uniquement le coefficient (ie, intercept=0).
Code:
def hypothesis(theta,x):
return theta*x
def cost_function(theta,x,y):
hypo=hypothesis(theta,x)
cf=(sum(pow((hypo-y),2)))/(2*len(x))
return cf
def gradient_descent(learning_step,start_theta,no_of_iterations,x,y):
thetas=[]
cost_functions=[]
theta=start_theta
m=len(x)
thetas.append(theta)
cost_functions.append(cost_function(theta,x,y))
for i in range(no_of_iterations):
h=hypothesis(theta,x)
new_theta=theta-((learning_step/m)*(sum((h-y)*x)))
theta=new_theta
cf=cost_function(theta,x,y)
thetas.append(theta)
cost_functions.append(cf)
return thetas,cost_functionsRésultat:
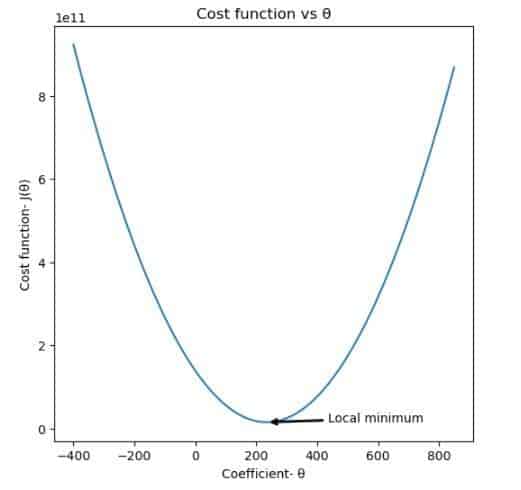
Fonction de coût
Faites défiler pour continuer
Le graphique ci-dessus montre la fonction de coût tracée pour un ensemble de coefficients allant de -400 à 850. On peut observer que la fonction de coût minimise une certaine valeur de coefficient.
t,c=gradient_descent(0.00000001,-400,100,X_train,Y_train)
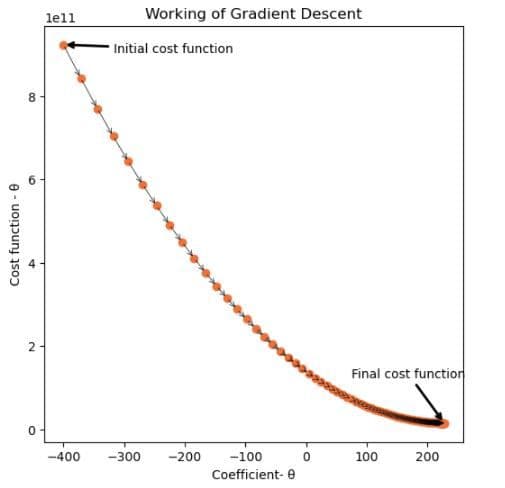
Descente en dégradé – 1
Ici, la descente de gradient commence avec une valeur de coefficient égale à -400 et fonctionne de manière itérative pour faire baisser la valeur de la fonction de coût sur 100 itérations.
t,c=gradient_descent(0.00000001,800,100,X_train,Y_train)
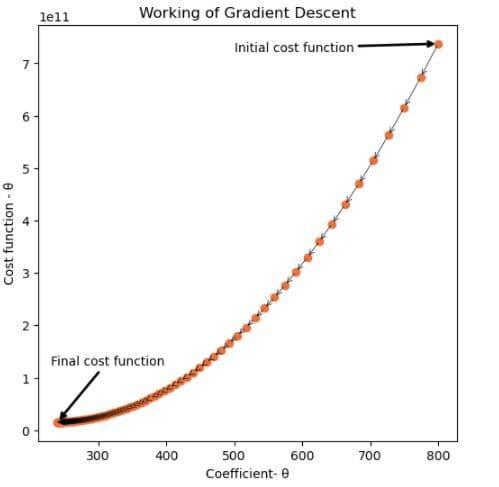
Descente en dégradé – 2
Dans ce cas, la descente de gradient commence par une valeur égale à 800 et s’étend sur 100 itérations.
Les deux cas fonctionnent sur la même valeur de pas d’apprentissage.
Comment la descente de gradient peut-elle fonctionner dans deux directions différentes ?
Vous devez vous demander pourquoi cela fonctionne différemment dans les deux cas ci-dessus. Les cas ci-dessus montrent clairement que la descente de gradient peut fonctionner dans deux directions différentes. Dans la parcelle 1, cela fonctionne de gauche à droite tandis que dans la parcelle 2, cela fonctionne de droite à gauche.
Cela est dû au terme dérivé qui est soustrait de la valeur initiale du coefficient (Reportez-vous à l’algorithme de descente de gradient dans la section Fonctionnement de la descente de gradient).
Cette dérivée est simplement la pente de la courbe en tout point. Dans le premier cas, la pente de la courbe est négative, ce qui se traduit par l’ajout d’un terme positif au coefficient. Par conséquent, la valeur du coefficient augmente dans les itérations suivantes. Dans le second cas, la pente de la courbe est positive, donc la valeur du coefficient ne cesse de décroître.
Que se passe-t-il si le pas d’apprentissage de la descente de gradient est réglé trop haut ?
t,c=gradient_descent(0.0000005,-400,10,X_train,Y_train)
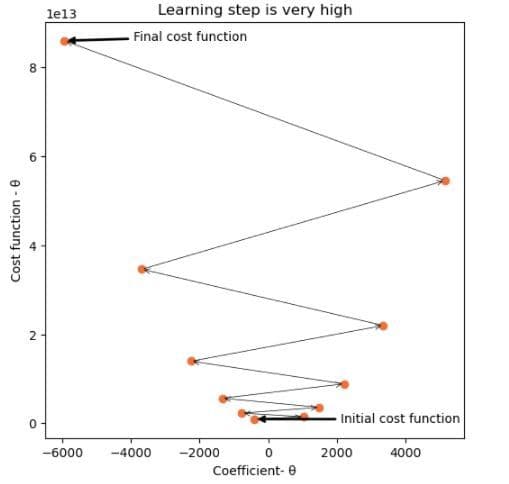
La valeur du pas d’apprentissage est trop élevée
Pour que la descente de gradient fonctionne correctement, il est important de définir le pas d’apprentissage sur une valeur appropriée. Un taux d’apprentissage élevé signifie de grandes étapes.
Si l’étape d’apprentissage est trop élevée, l’algorithme peut ne jamais être en mesure d’atteindre le minimum local car il rebondit entre la fonction convexe comme dans le scénario ci-dessus.
Si le taux d’apprentissage est très faible, l’algorithme finira par trouver le minimum local. Cependant, cela peut fonctionner assez lentement.
2. Modélisation avec intercept
Ici, nous considérons à la fois le coefficient et l’ordonnée à l’origine pour assumer une valeur finie.
Code:
def hypothesis2(coef,intercept,x):
return coef*x+intercept
def cost_function2(coef,intercept,x,y):
hypo=hypothesis2(coef,intercept,x)
cf=(sum(pow((hypo-y),2)))/(2*len(x))
return cf
def gradient_descent2(learning_step,start_coef,start_intercept,no_of_iterations,x,y):
coefs=[]
intercepts=[]
cost_functions=[]
coef=start_coef
intcp=start_intercept
m=len(x)
coefs.append(coef)
intercepts.append(intcp)
cost_functions.append(cost_function2(coef,intcp,x,y))
for i in range(no_of_iterations):
h=hypothesis2(coef,intcp,x)
new_coef=coef-((learning_step/m)*(sum((h-y)*x)))
coef=new_coef
new_intcp=intcp-((learning_step/m)*(sum((h-y))))
intcp=new_intcp
cf=cost_function2(coef,intcp,x,y)
coefs.append(coef)
intercepts.append(intcp)
cost_functions.append(cf)
return coefs,intercepts,cost_functionsRésultat:
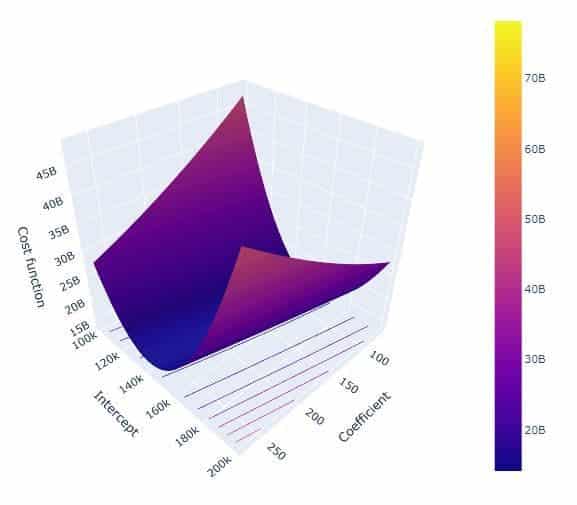
Fonction de coût
Dans ce cas, la fonction de coût dépend non seulement du coefficient, mais aussi de l’ordonnée à l’origine.
Le graphique ci-dessus montre la fonction de coût tracée pour une plage de valeurs des coefficients et des interceptions. Notez que le graphique contient un minimum global.
L’image ci-dessus résume le fonctionnement de la descente de gradient lorsque le coefficient et l’interception participent.
On voit clairement que les deux paramètres sont mis à jour simultanément jusqu’à ce que la fonction de coût atteigne son minimum local.
Vérifiez vos connaissances :
Pour chaque question, choisissez la meilleure réponse. La clé de réponse est ci-dessous.
- La descente de gradient fonctionne en ______ mettant à jour les paramètres.
- La descente de gradient fonctionne très bien si le pas d’apprentissage est réglé sur une très grande valeur.
Corrigé
- simultané
- Faux
Interpréter votre score
Si vous avez 2 bonnes réponses : Bravo !
Ce contenu est exact et fidèle au meilleur de la connaissance de l’auteur et ne vise pas à remplacer les conseils formels et individualisés d’un professionnel qualifié.
© 2021 Riya Bindra










