Les convolutions discrètes, continues et circulaires peuvent être effectuées en quelques secondes dans Matlab® à condition que vous maîtrisiez le code impliqué et quelques autres éléments de base.

Ce tutoriel vise à :
- Démontrez les composants nécessaires du code utilisé pour effectuer la convolution dans Matlab de manière simplifiée.
- Visualisez les résultats en traçant des graphiques de fonctions alambiquées.
Ce didacticiel est organisé dans l’ordre suivant :
- Continue la convolution.
- Convolution discrète.
- Convolution circulaire.
Logique:
Le concept simple derrière votre codage devrait être de :
1. Définir deux fonctions discrètes ou continues.
2. Convoluez-les en utilisant la fonction Matlab ‘conv()’
3. Tracez les résultats en utilisant ‘subplot()’.
Convolution continue dans Matlab
Nous allons le démontrer en utilisant deux fonctions continues :
- Une forme d’onde d’impulsion. Désigné par la fonction ‘square()’. C’est l’entrée x
- Réponse transitoire d’un condensateur. Désigné par une équation de la forme a*e1/RC*t. Cela pourrait être considéré comme la réponse impulsionnelle h
Code Matlab pour la convolution
tint = 0; tfinal = 0.05; tstep = 0.0005; t = tint : tstep : tfinal; x = 4 * square( 500*t, 50 ); //Use a function of your choice here. subplot( 3, 1, 1); plot( t, x); h = 400 * exp( (-400*t) ); //Use a function of your choice. subplot( 3, 1, 2); plot( t, h); t2 = 2*tint : tstep : tfinal*2; //Convoluted function requires a wider range to be plotted completely. y = conv( x, h) * tstep; subplot( 3, 1, 3); plot( t2, y);
Lignes 1 à 5 : Définissez la plage de valeurs pour l’axe du temps.
Ligne 7 : Une onde carrée est initialisée en utilisant la fonction Matlab ‘carré()‘ il a une amplitude de 4, ω = 500 rad/s et un rapport cyclique de 50 %.
Ligne 9 : sous-parcelle() partitionne la fenêtre de sortie pour accueillir 3 tracés sur un seul écran, c’est-à-dire qu’il crée un tableau de 3 lignes et 1 colonne(s) puis le dernier argument dans sous-parcelle() sélectionne la 1ère parcelle pour un travail ultérieur.
Faites défiler pour continuer
Ligne 10 : du coup x
b = 0; //Starting value of time for h
x = [ 2 -1 1];
h = [ 3 2 1];
subplot( 3, 1, 1);
t = a : a+length(x)-1; //tstep is not required here.
stem( t, x);
subplot( 3, 1, 2);
t = b : b+length(h)-1;
stem( t, h);
y = conv( x, h);
subplot( 3, 1, 3);
t = a+b : a+b+length(y)-1;
stem( t, y);
Lignes 4-5 : Définissez des valeurs discrètes pour x
Code Matlab pour la convolution circulaire
// Define two vectors for circular convolution
x = [2 5 4 1];
y = [1 4 3];
// Zeropad vectrs uptill 4+3-1
xpad = [x zeros( 1, 6-length(x) )];
ypad = [y zeros( 1, 6-length(y) )];
// Multiply ffts of both vectors and take idft of product
ccirc = ifft( fft( xpad ).*fft( ypad ) );
// Now plot result
stem( ccirc, 'filled' )
ylim( [0 35] )
title('Circular Convolution of xpad and ypad');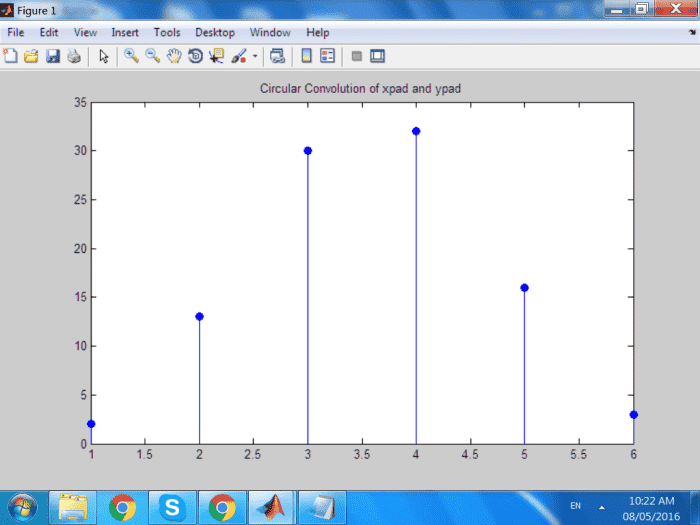
Convolution circulaire dans Matlab
© 2015 StormsHalted