La conversion des taux d’échantillonnage audio peut être un casse-tête pour les ingénieurs de diffusion.
Le défi de la conversion des taux d’échantillonnage
Les systèmes numériques utilisent un certain nombre de taux d’échantillonnage différents, ce qui peut causer des problèmes si vous avez l’intention d’utiliser un taux d’échantillonnage différent. En tant qu’ancien ingénieur de radiodiffusion, cela posait un certain nombre de défis. Nous avions souvent de l’audio numérique à 44,1 kHz, qui devait être converti en 48 kHz ou vice versa. D’autres fréquences d’échantillonnage devaient également être converties. Si vous envisagez un fonctionnement à vitesse variable, toutes les fréquences d’échantillonnage possibles peuvent être rencontrées. Par exemple, vous voudrez peut-être lire un podcast audio à une vitesse 1,5 fois supérieure afin de pouvoir l’écouter plus rapidement.
Une façon de convertir les fréquences d’échantillonnage consiste à reconvertir le signal en analogique, puis à le rééchantillonner numériquement à la fréquence d’échantillonnage souhaitée, mais cela est inutile et inutile.
Vous êtes-vous déjà demandé comment c’est fait correctement? Je l’ai fait, et c’est pourquoi j’ai préparé cet article pour vous.
Cet article commence par regarder les principes de base, en utilisant un exemple simple de conversion de 32kHz à 48kHz. Il met ensuite en évidence comment la technique peut être étendue à des cas plus difficiles.
Spectre de fréquence des signaux échantillonnés
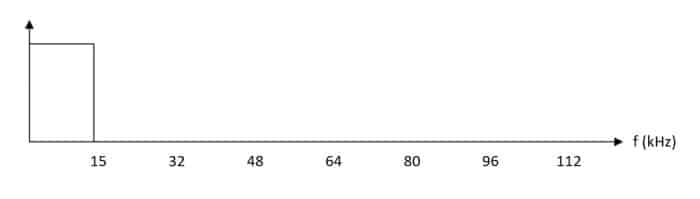
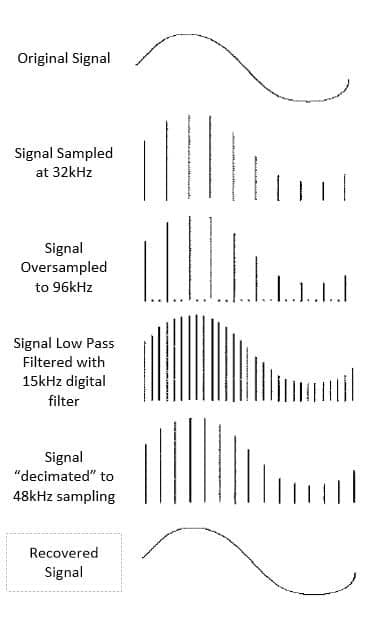
Audio 15 kHz
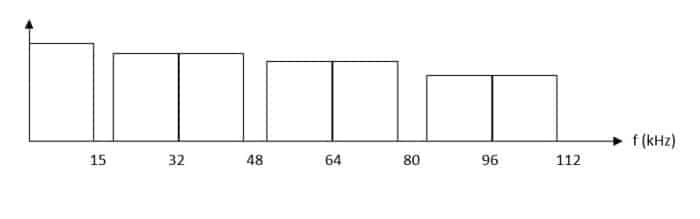
Audio 15 kHz échantillonné à 32 kHz
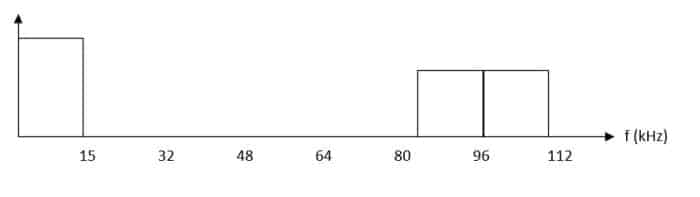
Audio 15 kHz échantillonné à 96 kHz
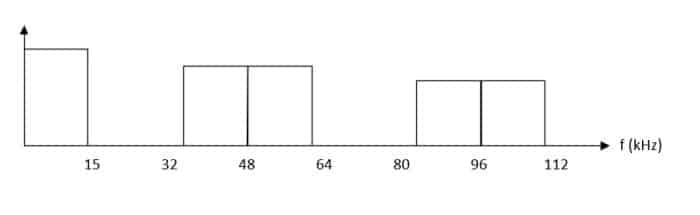
Audio 15 kHz échantillonné à 48 kHz
Un signal échantillonné contient le signal de bande de base et une série de bandes latérales autour de multiples de la fréquence d’échantillonnage. Toutes les informations nécessaires requises pour reproduire avec précision le signal d’origine sont contenues dans le signal en bande de base.
Dans l’exemple ci-dessus, le même signal audio est échantillonné à 32 kHz, 48 kHz et 96 kHz. Chacune des bandes latérales a une largeur de 15 kHz.
« Gearbox » Conversion de fréquence d’échantillonnage fixe
Considérez le processus de conversion de 32 kHz à 48 kHz.
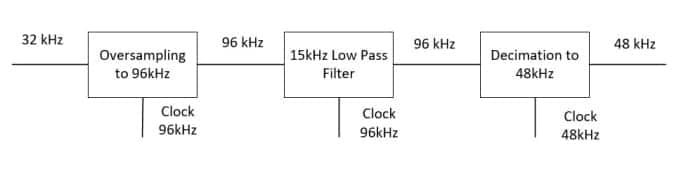
Si le signal est rééchantillonné à une fréquence plus élevée (96 kHz), qui est le plus petit commun multiple des fréquences d’échantillonnage d’origine et finale, aucune information ne sera perdue car certains des nouveaux points d’échantillonnage (tous les tiers) coïncideront avec ceux d’origine. .
Affichage de l’heure du processus de conversion
Filtre numérique
Le signal est maintenant échantillonné à haute fréquence mais a des composantes correspondant au processus d’échantillonnage d’origine. En le faisant passer à travers un filtre passe-bas (numérique) de la même bande passante que l’audio d’origine (15 kHz), les bandes latérales causées par le processus d’échantillonnage d’origine seront supprimées. Le signal en bande de base sera inchangé par ce processus.
La théorie de l’échantillonnage stipule que ce filtre passe-bas générera les échantillons manquants avec précision comme si le signal avait été échantillonné à un taux élevé à l’origine. En effet, le signal est limité en bande passante et toutes les informations nécessaires sont contenues dans les échantillons d’origine.
Décimation
Le signal à taux d’échantillonnage élevé (96 kHz) peut maintenant être rééchantillonné (à 48 kHz) pour générer la sortie requise. Ce processus implique de rejeter tous les autres échantillons et est appelé « décimation ».
Ainsi, nous sommes passés de 32kHz à 48kHz (mais avec une bande passante de seulement 15kHz). Il n’est pas possible de générer de nouvelles informations pour augmenter la bande passante.
Ces convertisseurs sont parfois appelés convertisseurs « boîte de vitesses » car ils fonctionnent à un taux fixe – les fréquences d’échantillonnage entrantes et sortantes doivent être verrouillées ensemble.
Conversion d’autres fréquences d’échantillonnage
Ce processus peut être utilisé pour convertir de 48 kHz à 32 kHz en effectuant l’inverse du processus ci-dessus, mais un filtre supplémentaire est nécessaire pour réduire les signaux originaux de 20 kHz aux 15 kHz requis avec une fréquence d’échantillonnage de 32 kHz.
De la même manière, 48 kHz et 44,1 kHz pourraient être interchangés. Le signal doit être rééchantillonné à 7,056 MHz, car il s’agit du plus petit commun multiple de ces fréquences.
Ces convertisseurs peuvent produire des résultats précis, limités par la résolution du traitement du signal effectué. Avec cette réserve, le processus devrait être transparent.
Conversion de fréquence d’échantillonnage variable
Si une conversion de fréquence d’échantillonnage variable doit être tentée, une approche légèrement différente est requise. Plutôt que d’utiliser l’approche « boîte de vitesses », l’approche à taux d’échantillonnage variable est utilisée, éliminant le besoin de verrouiller l’équipement pour des fréquences précises.
Le signal d’origine est rééchantillonné à une fréquence élevée, qui peut ne pas être un multiple exact de la fréquence d’échantillonnage entrante. Ce signal est ensuite passé à travers un filtre numérique variable. Les caractéristiques du filtre changent pour s’adapter au rapport variable entre les taux d’échantillonnage entrant et sortant. La sortie du filtre est « décimée » pour la ramener au taux requis.
Étant donné que la fréquence d’échantillonnage élevée n’est pas un multiple exact de la fréquence d’échantillonnage d’origine, il ne s’agit pas d’un processus exact. Cependant, en réduisant les erreurs d’arrondi dans le traitement du signal, la dégradation peut être minimisée.
Ce contenu est exact et fidèle au meilleur de la connaissance de l’auteur et ne vise pas à remplacer les conseils formels et individualisés d’un professionnel qualifié.
© 2022 Monsieur Singh