Joshua est étudiant diplômé à l’USF. Il s’intéresse à la technologie d’entreprise, à l’analyse, à la finance et au lean six sigma.
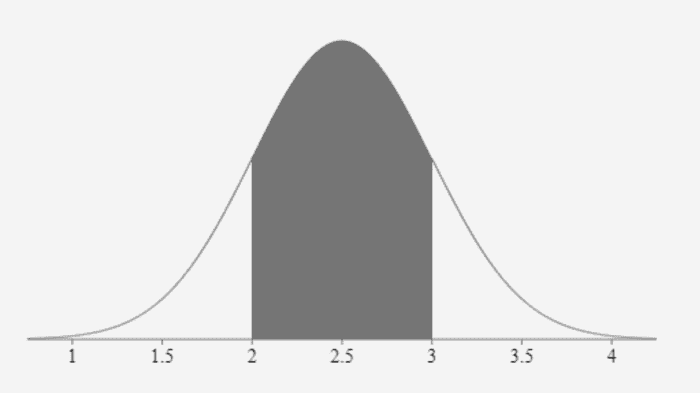
Une distribution normale est également appelée distribution gaussienne, gaussienne ou distribution de Laplace-Gauss.
Créé par Joshua Crowder
Distribution normale
La distribution normale est une distribution de probabilité continue très courante dans la théorie des probabilités. La distribution normale est souvent appelée courbe en cloche, même si d’autres distributions ont également une courbe en forme de cloche. Cette distribution est utile car les propriétés du théorème central limite permettent son utilisation dans de nombreuses applications.
Fonction de distribution normale d’Excel (fonction NORM.DIST)
La fonction de distribution normale affiche la distribution normale lorsqu’une moyenne, un écart type, une valeur x et une détermination de fonction spécifiés sont ajoutés à la fonction. L’utilisation de cette fonction se trouve principalement dans les statistiques pour déterminer l’aire dans une distribution normale. Le test d’hypothèse, qui relève du domaine inférentiel des statistiques, est l’endroit où vous trouverez une large utilisation de cette fonction. Une description de la syntaxe NORM.DIST est affichée dans le tableau ci-dessous.
Syntaxe de la fonction de distribution normale
Exemple de queue gauche
Disons simplement par exemple qu’une entreprise a une valeur de vente moyenne de 2,5 millions de dollars. Supposons également que les ventes soient normalement distribuées avec un écart type de 0,5 million et que nous souhaitions connaître le pourcentage de ventes inférieur à 3,5 millions. Lorsque nous insérons nos nombres dans une cellule = NORM.DIST (3,5, 2,5, 0,5, vrai), nous obtenons 0,977 en conséquence. Vrai est sélectionné pour le type de fonction car nous voulons voir la distribution cumulée jusqu’au point de 3,5.
Étant donné que l’exemple indique que nous voulons trouver le pourcentage de ventes inférieur ou inférieur à 3,5, nous savons que nous calculons le pourcentage dans la queue de gauche. Lorsque cette fonction est utilisée pour calculer la queue gauche, aucun autre calcul n’est autorisé après l’utilisation de la fonction NORM.DIST.
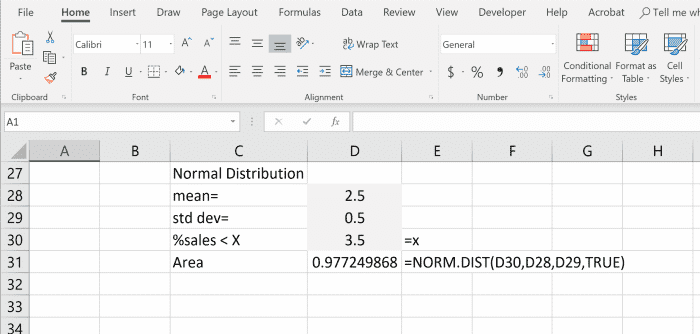
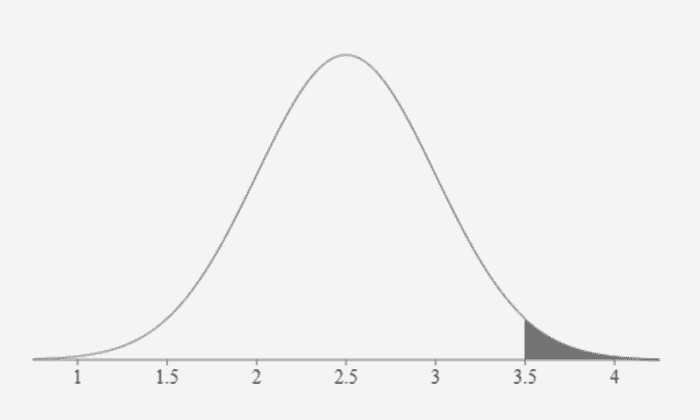
Puisque nous recherchons ce qui est inférieur à x dans l’exemple, nous recherchons la zone à gauche de notre valeur x.
Créé par Joshua Crowder
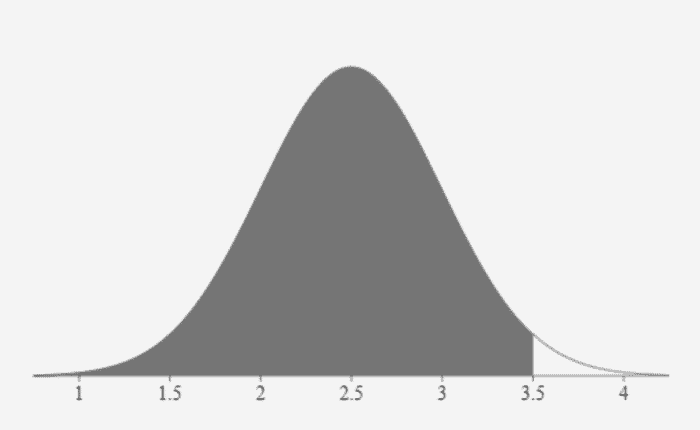
La zone ombrée dans cette distribution montre la zone de 0,977 qui a été calculée. La zone à droite peut maintenant être calculée avec cette opération 1 – .977 = .023
Créé par Joshua Crowder
Exemple de queue droite
Cet exemple est similaire à l’exemple de la queue gauche car les mêmes données sont utilisées. La valeur moyenne des ventes est de 2,5 millions de dollars, les ventes sont normalement distribuées, l’écart type est de 0,5 million de dollars et la valeur de x est de 3,5 millions de dollars. La différence ici est que nous voulons trouver le pourcentage des ventes au-dessus de 3,5 millions.
Essentiellement, pour pouvoir trouver cette valeur, nous devons trouver la même distribution cumulative que dans l’exemple précédent et la soustraire de 1. Ainsi, la fonction apparaît comme ceci : =1-NORM.DIST(3.5,2.5,.5,true ). Comme on cherche tout dans la queue droite (supérieur à 3,5), il suffit de calculer le complément de la queue gauche.
Faites défiler pour continuer
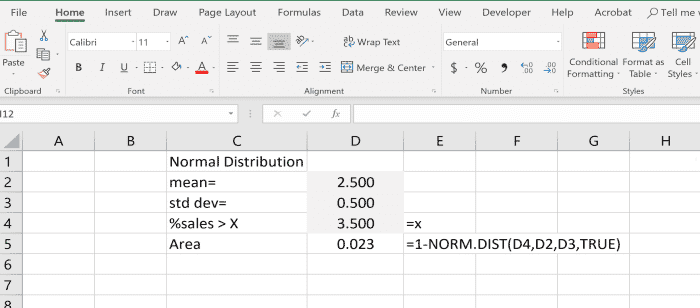
Notez que l’exemple ci-dessus montre les références de cellule dans la fonction au lieu des nombres réels. Lorsque vous créez votre fonction Excel, vous pouvez cliquer dans la cellule de la valeur souhaitée au lieu de taper la valeur réelle pour créer la fonction plus rapidement.
Créé par Joshua Crowder
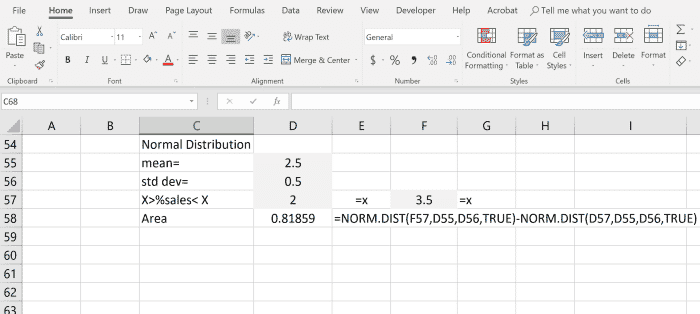
Pour calculer la queue droite, vous devez d’abord calculer la queue gauche et soustraire cette fonction de 1. La zone ombrée ci-dessus montre la zone (.023) qui a été calculée pour la queue droite.
Créé par Joshua Crowder
Exemple de zone centrale
La zone centrale peut sembler difficile à calculer pour certaines personnes. Dans cet exemple, disons que nous utilisons toujours 2,5 millions de dollars pour les ventes moyennes, les ventes sont normalement distribuées et l’écart type est de 0,5 million de dollars. La seule différence maintenant est que nous devons trouver le pourcentage des ventes entre 2 et 3,5 millions de dollars.
En regardant les illustrations de distributions précédentes ci-dessus, pouvez-vous comprendre comment trouver la zone centrale ? Vous devez simplement trouver la zone jusqu’à 3,5 millions de dollars, puis soustraire cette zone par la zone qui apparaît en dessous de 2. Le fonctionnement de la fonction, dans ce cas, ressemble à ceci =NORM.DIST(3.5,2.5,.5,true )-NORM.DIST(2,2.5,.5,vrai). Ceci est explicite. En soustrayant toute la zone à gauche de 3,5 par la zone à gauche de 2, vous vous retrouverez avec le centre.
Pour trouver la surface totale de chacune des queues, vous pouvez soustraire la surface au centre de un.
Créé par Joshua Crowder
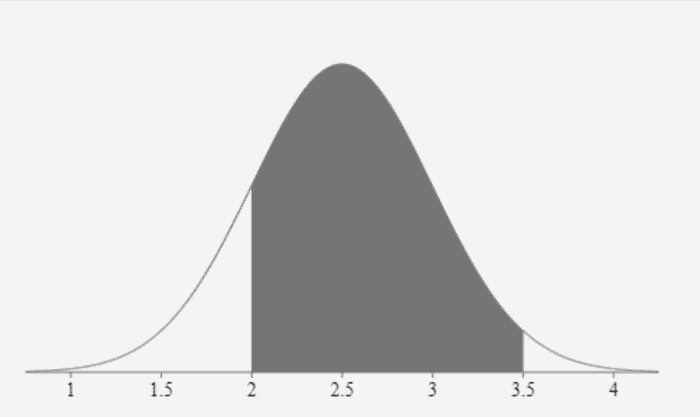
L’ombré dans la distribution normale ci-dessus est le résultat de la soustraction de la queue inférieure de la distribution cumulative de 3,5.
Créé par Joshua Crowder
Pour en savoir plus sur la réalisation de calculs statistiques dans Excel, je vous suggère d’essayer de lire la Bible Excel. C’est un bon livre de référence pour les utilisateurs débutants d’Excel.
Références
- Fonction NORM.DIST. (sd). Extrait le 15 octobre 2018 de https://support.office.com/en-us/article/norm-dist-function-edb1cc14-a21c-4e53-839d-8082074c9f8d
- distribution normale. (2018, 10 octobre). Extrait le 15 octobre 2018 de https://en.wikipedia.org/wiki/Normal_distribution
Ce contenu est exact et fidèle au meilleur de la connaissance de l’auteur et ne vise pas à remplacer les conseils formels et individualisés d’un professionnel qualifié.
© 2018 Josué Crowder