Joshua est étudiant diplômé à l’USF. Il s’intéresse à la technologie d’entreprise, à l’analyse, à la finance et au lean six sigma.

Les statistiques descriptives décrivent les caractéristiques des données en fournissant des résumés sur l’échantillon ou la population étudiée. Avec l’analyse graphique, les statistiques descriptives forment la base de la plupart des analyses quantitatives des données.
Créé par Joshua Crowder
Excel rend le calcul des statistiques beaucoup plus facile aujourd’hui que jamais. Il faut littéralement quelques frappes et quelques clics pour obtenir à peu près n’importe quel type de mesure statistique ou de graphique à partir d’un ensemble de données. Excel est préchargé avec des fonctions statistiques qui peuvent vous aider à trouver la moyenne, la médiane, le mode, la variance et bien d’autres mesures statistiques.
Outre les fonctions d’Excel, le programme permet également aux utilisateurs d’installer un complément Data Analysis ToolPak qui est utilisé pour effectuer plusieurs types de calculs à la fois. Ce didacticiel montre à un utilisateur Excel comment utiliser l’outil d’analyse de données pour trouver des statistiques descriptives et explique les résultats.
Si vous n’avez jamais utilisé le Data Analysis ToolPak, il est probablement inactif sur votre programme Excel. Vous pouvez vérifier si vous l’avez en cliquant d’abord sur l’onglet des données, puis recherchez le groupe d’analyse à l’extrême droite de votre écran. Si l’option d’analyse des données n’existe pas, procédez comme suit pour activer ce complément.
- Cliquez sur l’onglet Fichier, puis cliquez sur les options. Ensuite, cliquez sur « Compléments ».
- Ensuite, cliquez sur le bouton « Aller » pour accéder à la section de gestion des compléments.
- Enfin, cochez la case « Analysis Pak » et cliquez sur « OK ».
Vous devriez maintenant être prêt à utiliser le Data Analysis ToolPak à partir de l’onglet de données dans le groupe d’analyse.
Exemple d’analyse de données
Si vous suivez cet exemple avec une feuille de calcul Excel, saisissez cet ensemble de données dans Excel verticalement dans des cellules individuelles.
2, 5, 7, 9, 4, 3, 3, 4, 6, 8, 14, 4, 20, 6, 10, 4, 5, 9, 11, 1, 6, 9, 4, 5, 13, 18, 7, 6, 9, 10
Cliquez sur « Analyse des données » dans l’onglet des données, puis cliquez sur Statistiques descriptives dans la boîte de dialogue. Cliquez sur le bouton OK.
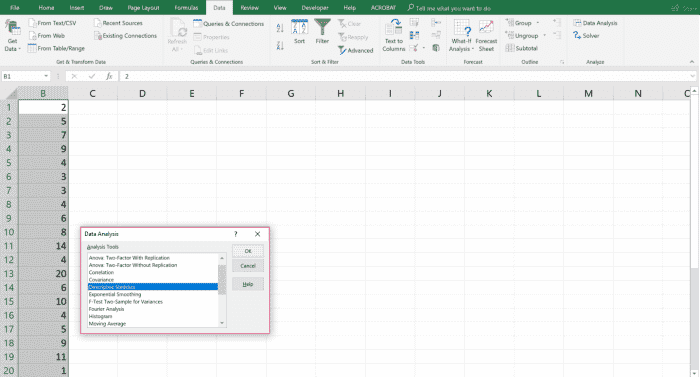
Avec le pack d’outils d’analyse de données, vous pouvez fournir des données et des paramètres pour chaque analyse, et l’outil de données utilise les bonnes macros statistiques dans Excel pour calculer les résultats dans un tableau en sortie.
Créé par Joshua Crowder
Ensuite, la plage des données doit être saisie dans la section plage d’entrée de la boîte de dialogue. Choisissez l’option de plage de sortie et choisissez une cellule pour la sortie à afficher en tapant cet emplacement de cellule dans le champ vide. Enfin, cochez la case Résumé des statistiques et cliquez sur OK pour afficher les résultats.
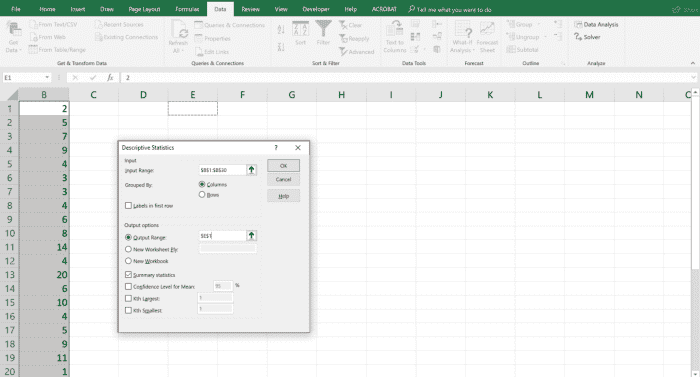
À l’aide de l’outil d’analyse Statistiques descriptives, un rapport peut être généré qui affiche des statistiques univariées pour les données dans la plage d’entrée. Ces données renseignent sur la tendance centrale et la variabilité des données utilisées.
Créé par Joshua Crowder
Les résultats
Les résultats s’impriment sur deux colonnes. La première colonne représente la statistique descriptive et la deuxième colonne affiche les résultats de ces statistiques. Dans les sections suivantes, je décrirai ce que représentent ces statistiques descriptives.
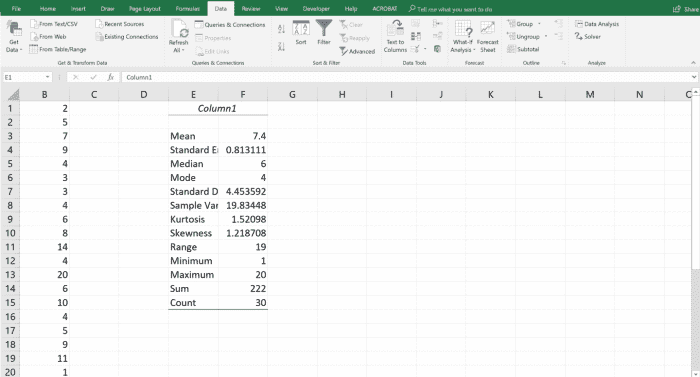
L’outil Statistiques descriptives affiche 13 résultats statistiques afin que vous puissiez faire une analyse rapide.
Créé par Joshua Crowder
moyenne
La moyenne, qui est une mesure de la tendance centrale, a été calculée en prenant la moyenne de l’ensemble des données. La somme de l’ensemble de données est de 222 et, lorsqu’elle est divisée par 30, donne une moyenne de 222/30 = 7,4. La moyenne peut être écrite comme l’expression : ∑xi /n, où n est le nombre de valeurs et ∑xi est la somme des valeurs de données.
Faites défiler pour continuer
Erreur standard
L’erreur type est définie comme l’écart type divisé par la racine carrée de la taille de l’échantillon. Dans l’exemple ci-dessus, l’erreur type est de 4,45/sqrt(30) = 0,813.
La médiane est la valeur médiane et une autre mesure de la tendance centrale. Pour trouver la valeur médiane ou médiane de l’ensemble de données, vous devez organiser l’ensemble de données dans l’ordre croissant ou décroissant. La valeur médiane est directement au milieu lorsqu’il y a un nombre impair de valeurs dans l’ensemble de données. Lorsqu’il y a un nombre pair de valeurs, il y aura deux valeurs moyennes qui devront être moyennées pour trouver la médiane.
Mode
Une autre mesure de tendance centrale est la mode. Il s’agit de la valeur qui apparaît plus fréquemment que toute autre valeur. Dans l’exemple ci-dessus, 4 apparaît plus que tout autre nombre. Il peut y avoir un cas où il y a plus d’une mode. Cela se produit lorsque deux nombres apparaissent le plus fréquemment dans un ensemble de données mais apparaissent le même nombre de fois.
Écart-type
L’écart type est la racine carrée du résultat de la variance. Il existe deux scénarios selon que l’écart-type est calculé à partir d’une population ou d’un échantillon. Pour un écart-type de population, le calcul mathématique est sqrt(∑(xi-Xbar)2/n). Lors du calcul de l’écart type pour un échantillon, le calcul est sqrt(∑(xi-Xbar)2/(n-1)). Dans l’exemple ci-dessus, l’écart-type de la population est de ou 4,378. L’écart type de l’échantillon est la racine carrée de ou 4,453.
Variance
La variance est trouvée en calculant l’écart de chaque valeur par rapport à la valeur moyenne. Ensuite, mettre au carré l’écart et trouver la moyenne de ces écarts au carré. Pour simplifier, la variance est l’écart quadratique moyen. L’équation pour calculer la variance de la population est ∑(xi-Xbar)2/n pour une population et pour une variance d’échantillon ∑(xi-Xbar)2/(n-1). Dans l’exemple ci-dessus, la variance de la population est de 19 173 (575,2/30) et la variance de l’échantillon est de 19 834 (575,2/29).
Aplatissement
L’aplatissement est une mesure de distribution. Il nous indique le pic ou l’étroitesse de la distribution. Une valeur d’aplatissement élevée signifie que le pic de la distribution est élevé. Un aplatissement négatif nous indique que la distribution a un pic plus arrondi. Dans l’exemple ci-dessus, l’aplatissement est de 1,52.
asymétrie
L’asymétrie mesure l’asymétrie d’une distribution. Les données symétriques ont des données distribuées symétriquement autour de la moyenne. S’il est parfaitement symétrique, nous dirions que l’asymétrie d’une distribution est nulle. Une distribution est positivement asymétrique, ou vers la droite, si la queue droite est plus longue. Si la queue gauche est plus longue, on dit que la distribution est asymétrique négativement ou asymétrique vers la gauche. Dans l’exemple, l’asymétrie est de 1,218. En conséquence, on peut dire que les données sont biaisées vers la droite ou sont positivement biaisées ou ont une longue queue droite.
intervalle
La plage correspond à la valeur la plus élevée de l’ensemble de données moins la valeur la plus faible. Dans l’exemple ci-dessus, la plage est de 20 (le plus élevé) moins 1 (le plus bas), ce qui équivaut à 19.
Min et Max
Le min et le max sont respectivement les valeurs les plus basses et les plus hautes de l’ensemble de données. Dans l’exemple ci-dessus, la valeur la plus élevée est 20 et la plus faible est 1.
somme
La somme ou ∑ est simplement l’addition de tous les nombres de l’ensemble de données. Dans l’exemple ci-dessus, la somme est 222.
compter
Le nombre est simplement la taille de la population ou la taille de l’échantillon. Dans l’exemple, le compte est de 30.
Tutoriel vidéo sur les statistiques descriptives
Ce contenu est exact et fidèle au meilleur de la connaissance de l’auteur et ne vise pas à remplacer les conseils formels et individualisés d’un professionnel qualifié.
© 2018 Josué Crowder
Pierre Westfall le 22 juin 2020 :
En fait, l’aplatissement ne mesure rien de la forme du pic. Les données proches du pic ont très peu d’effet sur l’aplatissement. Au lieu de cela, l’aplatissement ne mesure que les queues (en particulier, les valeurs aberrantes ou le potentiel de valeur aberrante). Voir la page Wikipedia actuelle pour plus d’informations. L’interprétation « pics/planéité » est une erreur historique.